Содержание:
В мире анализа данных и статистики одним из ключевых понятий, которое часто обсуждается и используется для оценки качества прогнозов, является RMSE (среднеквадратическая ошибка). Этот показатель служит важным инструментом для аналитиков и исследователей, работающих с временными рядами, позволяя им эффективно оценивать качество своих моделей. Понимание RMSE и его значимости является необходимым шагом к созданию надёжных предсказательных моделей.
Что такое RMSE?
RMSE — это одна из наиболее распространённых метрик, применяемых для оценки ошибок прогнозов. Она вычисляется как квадратный корень среднего значения квадратов разностей между предсказанными и фактическими значениями. Этот показатель не только показывает, насколько точно выполнены прогнозы, но и позволяет придавать им отличие между положительными и отрицательными ошибками, что является важным аспектом при исследовании временных рядов.
Формула расчёта RMSE
Формула для вычисления RMSE выглядит следующим образом:
RMSE = √(1/n * Σ(actual — predicted)²)
Где:
- n — количество предсказаний;
- actual — фактические значения;
- predicted — предсказанные значения;
- Σ — символ суммы, который обозначает суммирование всех разностей.
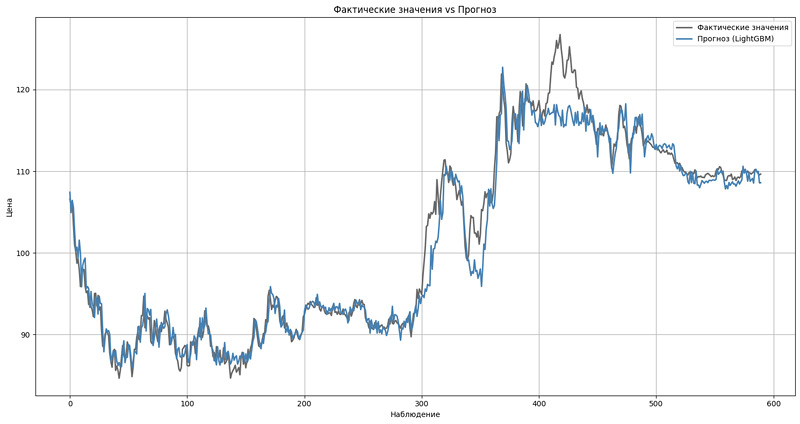Значение RMSE в оценке качества прогнозов временных рядов
При работе с временными рядами точность прогнозирования имеет критическое значение, поскольку она непосредственно влияет на принятие бизнес-решений и стратегий. Используя RMSE, аналитики могут:
1. Сравнивать различные модели прогнозирования
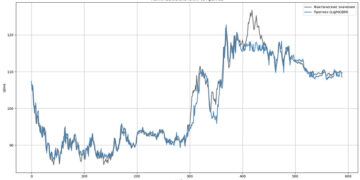
Анализируя RMSE для разных моделей, можно определить, какая из них лучше справляется с задачей предсказания. Меньшее значение RMSE указывает на более точные прогнозы.
2. Оценивать точность моделей при тестировании
После разработки модели очень важно проверить её на тестовых данных. Поэтому RMSE предоставляет чёткое измерение её точности, указывая, насколько хорошо модель может предсказывать непредвиденные данные.
3. Упрощать интерпретацию ошибок
RMSE даёт понятное представление об ошибках в предсказаниях, что позволяет аналитикам быстро оценить, какие значения находятся далеко от фактических. Это критически важно для принятия корректирующих мер и оптимизации моделей.
Преимущества и недостатки использования RMSE
Преимущества RMSE
- Простота расчёта: Расчёт RMSE не требует сложных вычислений и легко осуществим в любом статистическом пакете.
- Чувствительность к выбросам: RMSE подчеркивает влияние больших ошибок, что позволяет выявить аномалии в данных.
- Наилучшее использование с нормальными распределениями: RMSE хорошо работает с моделями, основанными на предположении о нормальном распределении ошибок.
Недостатки RMSE
- Чувствительность к выбросам: С одной стороны, это преимущество, но с другой — может исказить оценку качества модели, если в данных присутствуют экстремальные значения.
- Не отражает симметричность ошибок: RMSE не различает направление ошибок, что может быть важно в определенных контекстах.
- Требует интерпретации в контексте: Высокое значение RMSE может быть нормой для одной области, но критическим для другой, что делает его метрикой, требующей контекста.
Заключение
Суммируя, RMSE является важным инструментом для оценки качества прогнозов временных рядов. Он предоставляет целостное представление о точности предсказаний и позволяет исследователям и аналитикам принимать обоснованные решения при разработке и внедрении прогнозирующих моделей. Хотя у RMSE есть свои плюсы и минусы, его значение в мире научных исследований и бизнес-аналитики невозможно переоценить. Понимание и использование этой метрики может значительно повысить качество прогнозов и привлечь внимание к важным аспектам данных.
